Introduction
Finding the Power Set of a String can be tricky if you are unfamiliar with solving recursive problems.
However, this also makes it a good opportunity to learn about how to identify recursive problems in the wild, and how to break them down so that they are easier to solve.
A Primer in Combinatorics
This problem lends itself to being solved recursively because it’s related to a field of math called combinatorics. As the name implies, this is all about mixing and matching things. Usually, these are physical things, like colored balls, and it’s typically taught in relation to the field of statistics and probability, where it has the most practical implications.
So before we dive into the problem, it’s worth defining just what the Power Set is:
“It is the set of all subsets.”
Since we’re talking about strings, this means it’s the set of all substrings. But before going into more definitions, I think it’s useful to start with an example so you can get an intuitive understanding of what’s going on.
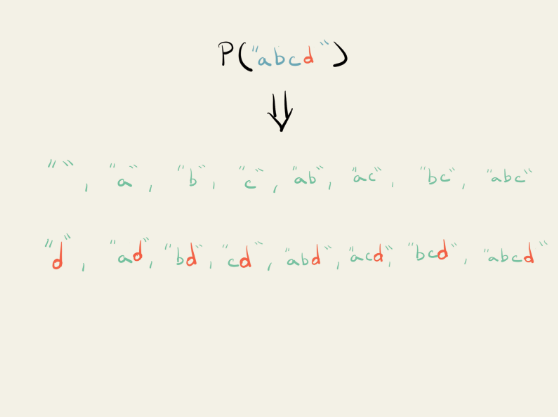
Let’s take the Power Set of the string “ABC.” The result we get is:
There’s probably a few things you’ll notice right off the bat about the result, and just doing this and taking notes about what you see is a good idea.
You want to notice that output is a list of strings. You might notice that there are 8 strings in this list and that these strings are of various different lengths. And just in doing this, you’ll probably have some follow up questions about the problem.
To list a few:
Does the order of strings in the list matter?
Does the order of characters in each string matter?
What’s the relationship between the length of the input string, and the number of strings in the output?
To answer these questions we’ll need to know about what sets are and some of their properties.
As an aside, most languages have some kind of native Set data structure, that behaves in exactly this way. It’s similar to how a hash table works, and essentially only has keys without values.
For our purposes, a set is simply an unordered collection of items. This is a pretty vague definition, but the keywords are “unordered collection.”
Since the power set is itself a set, that means the order of its items does not matter. This means that the order of elements in the array we return does not matter.
And since what we’re returning is a set of sets, it also means the order of the characters in the strings doesn’t matter, since we’re considering each string a set.
What this means is that we can return any permutation of a string that would appear in the final result and that all permutations are treated equally.
But the word permutation is worth pinning down, because I’ve heard it used by engineers interchangeably with the word combination, and this can often be a source of confusion since technically they mean different things.
In the context of strings, when talking about permutations, we’re talking about any shuffling of the order of their characters. All permutations are of the same length, and they contain the same characters. Two permutations are only equivalent if they have the same characters in the same positions. The number of unique permutations you can create from a string of N unique characters is N factorial, which is probably one of the fastest-growing complexities you’ll have to deal with.
Now when we’re talking about combinations, we’re talking about unique subsets, where the order doesn’t matter. We always need to specify the size of the subsets we’re creating. But how you order the items in each of those sets isn’t important.
So a question you could ask in the context of combinations might be “how many unique sets of 2 items can you create from this set of 10 items?” Put another way, “from N items how many ways can you choosing K of them?”
Calculating how many combinations you can make then depends on two factors: N, the total number of starting items, and K, the number of them that you are “choosing.” The formula isn’t quite as straightforward as the one for permutations, but it does involve factorials.
It’s called the Binomial Distribution Formula and it’s relevant in statistics and probability.
Combinations can never have more items in them than the set they are drawing from. But you can have combinations with no elements in them. This is kind of a weird notion, but every set has exactly 1 combination with no elements in it. We call this the empty set.
A funny thing about combinations is that if you take all the combinations of all the different sizes, then you actually end up with the Power Set of that original set. Those two notions are equivalent.
Seeing the Recursion
At this point, you’re probably wondering where recursion fits into this whole picture. If you’re at all familiar with the pattern of recursive functions, you know that we need a base-case and one or more recursive cases. You might also be familiar with helper-method recursion and the pattern of storing state variables outside of the helper function and then modifying those throughout the recursion to be returned at the end.
However, even though the solution to this problem follows a fairly standard pattern, knowing how to fit those pieces fit together might not be apparent at first. So the best way to get started is just by trying a few examples and then look for patterns.
Here is a list of some easy, intuitive ones to start with. A key thing to notice here is that there are a few ways to organize the outputs. I’ve chosen one in particular to highlight the pattern we’re going to leverage during the recursion. Can you see it?
Let’s try one more example, by adding another letter to the end. Trying to find patterns by incrementally changing the input is a good strategy for discovering the relationships between larger and smaller inputs, and how to go from one to another.
I’ve color-coded the new letter and arranged the output in a particular way to highlight the pattern.
Notice what’s happening. This is the pivotal point in the problem where we establish the key insights. Ideally, we can summarize our solution in a sentence or two of high-level pseudocode.
So if you had to describe this solution to your interviewer you might say something like:
Take the power set of the string up to the next character, make a copy of that result with that new character at the end of each string, and then merge those two sets.
If you were to express this a little more abstractly as a formula for this example, that might look like this:
And more generally:
So let’s try to analyze the complexity of this solution. In some cases, the interviewer will give you this as a constraint at the beginning, but in many cases, they’ll just leave it open and tell you to make it as efficient as possible.
Luckily, the power set, by definition, has an easy mathematical way of figuring out the number of elements in the output from an input of a given size. But we can derive that formula just by looking at the above formulas.
For every additional letter we add to our starting set, we need to make a copy of the power set up to that point, and then merge the two sets.
Another way of putting this is that when we increment the input size by one we automatically double the size of the output. We multiply by two.
Which means the power set of n elements will always have 2 to the power of n elements:
Implementing a Solution
The next question we need to answer is how to actually implement a program that solves this problem in code. I’ve mentioned in previous posts that we want to find something called a “unit of recursion.” Usually, if we’re returning something like an array, this corresponds to each element in the array.
Knowing the unit of recursion is useful because it helps us know what we will actually “return” or “append” at the end of our calculation. In this case, it’s each string in the result array. We just need to figure out how we’re actually building each one up.
Going back to our formula, we want a way of building on the solutions to power sets with fewer characters. Another way of thinking of this is that if we stopped our recursion early, our solution would still return a valid power set.
As such, whatever string we’re building up currently, needs to be copied, and then the character we want to add, needs to be added to one of those copies. Therefore we need two recursive calls, which corresponds to our intuition that this solution doubles in size for every additional character we add to our input:
As for our base case, we want to perform this task on all our characters before adding a string to our result array. Therefore:
We’ll be using helper-method recursion since this will allow us to keep track of more variables in our recursive calls and allows us to keep track of the array outside of our recursive function’s scope.
Since we’re building up strings, we’ll want to track the string we’ve built up so far as one of our parameters to the recursive function. And we’ll also want to keep track of what the next character we want to add from the set is. A good way to do this is just by keeping track of the index of that character.
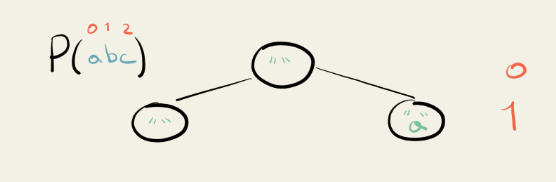
So, if we were to diagram the recursive tree for this problem we would first start with an empty string as the root node. This makes sense because the power set of the empty set is just the empty set itself. We’ll also diagram the index of the next character to add as the “layer” of the tree we are currently on.
Since the letter a is at the 0 index, it’s the first one to be added. The way we diagram this is as two branches. On one branch, we add the “a” and on the other, we skip over it.
We now have layer 1, and additionally, this is the power set of just the letter “a.”
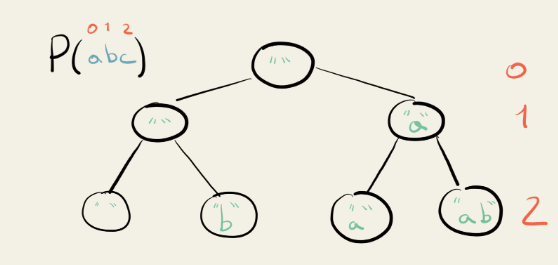
We repeat this process for the next letter, “b”. Again, for each node in layer 1, we need to make a copy with the letter “b” and a copy without it. This will give us:
Which, again, is the power set of the string “ab”.
Repeating this whole process one last time for the letter “c”, we finally get the power set of “abc”.
Now that we’re at the end of the process, let’s discuss the base case. Layer 3, corresponds to the length of the input string. It also corresponds to an index that is outside of the bounds of the string, so we won’t be able to add any characters from it. This means our base case is when the character index we want to add from equals the length of the input string.
One important thing to remember here is that we want to add the string we’ve built up so far in the recursion, and then return out of it. If we don’t, the code will try to execute the recursive calls after the base case and end up breaking.
As a final note, a couple of common small mistakes folks make are forgetting to actually invoke their helper method within their outer function. You actually have to kick-off the recursion at some point. You also have to return the array you’ve built up at the end since you won’t be returning anything directly from your helper method.
And that’s the whole problem. I’ve linked to the code below in a gist. Hopefully what’s happening at each step will be fairly easy to follow.
https://gist.github.com/spiterman/059600437f6e0c6f559a212266bf3062
Conclusion
Recursive problems can be tricky, but they're all about finding the patterns between larger and smaller inputs. Like most problems, this problem can actually be solved in a number of ways, and if you’re up for a challenge, I’d suggest trying to solve it without using any kind of recursion whatsoever.
And if you’re interested in Outco’s immersive accelerator program checkout outco.io. It’s a great way for engineers to speed up their job search and make it makes jumping through all the interview hoops less painful.
If you want to connect with me on social media feel free on any of these links:
If you want to check out some other popular posts:
How to Solve the House Robber Problem
Imagine you are a thief trying to steal as much gold from a neighborhood as possible.medium.com